Surface Areas and Volumes Class 10 Extra Questions Maths Chapter 13

 

NEW LEARNET EDUCATION

CHAPTER - 13 SURFACE AREAS AND VOLUME

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Question 1.
A sphere of diameter 18 cm is dropped into a cylindrical vessel of diameter 36 cm, partly filled with water. If the sphere is completely submerged, then calculate the rise of water level (in cm). (2011D)
Solution:
Volume of Cylinder = Volume of Sphere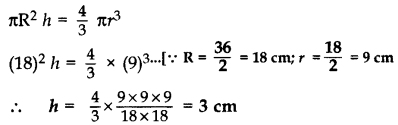

Question 2.
Find the number of solid spheres, each of diameter 6 cm that can be made by melting a solid metal cylinder of height 45 cm and diameter 4 cm. (2014D)
Solution:
Number of solid spheres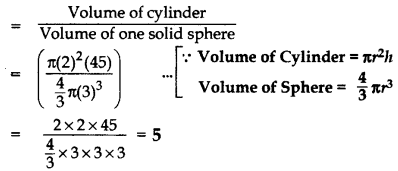

Question 3.
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. Find the ratio of the volume of the smaller cone to the whole cone. (2012OD)
Solution:
Since the cone is cut from the middle,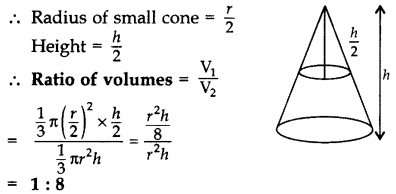

Question 4.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere? (2017D)
Solution:
Volume of hemisphere = Surface area of hemisphere …[Given
23πr3 = 2πr2 ⇒ 13r = 1
r = 3
∴ Diameter of hemisphere = 27 = 2(3) = 6 cm

Surface Areas and Volumes Class 10 Important Questions Short Answer-I (2 Marks)

Question 5.
If the total surface area of a solid hemisphere is 462 cm2, find its volume. [Take π = 227] (2014OD)
Solution:
Total surface area of hemisphere = 462 cm2

Surface Areas and Volumes Class 10 Important Questions Short Answer-II (3 Marks)

Question 6.
Two cubes, each of side 4 cm are joined end to end. Find the surface area of the resulting cuboid. (2011D)
Solution:
Length of resulting cuboid, I = 2(4) = 8 cm
Breadth of resulting cuboid, b = 4 cm
Height of resulting cuboid, h = 4 cm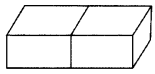

Surface area of resulting cuboid
= 2(lb + bh +hl) = 2 [8(4) + 4(4) + 4(8)]
= 2 (32 + 16 + 32) = 2 (80) = 160 cm2

Question 7.
The radii of the circular ends of a bucket of height 15 cm are 14 cm and r сm (r < 14 cm). If the volume of bucket is 5390 cm3, then find the value of r. [Use π = 227] (2011D)
Solution:
Here h = 15 cm, R = 14 cm,’r’ = r cm
Volume of bucket = 5390 cm3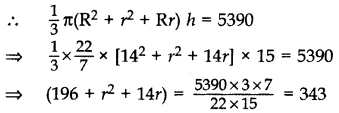

⇒ r2 + 14r + 196 – 343 = 0
⇒ r2 + 14r – 147 = 0 = r2 + 21r – 77 – 147 = 0
⇒ r(r + 21) – 7 (r + 21) = 0
⇒ (r + 21) (r – 7) = 0
⇒ r + 21 = 0 or r – 7 = 0 =
⇒ r = -21 (rejected) or r = 7
..[∵ Radius cannot be negative
∴ Radius, r = 7 cm

Question 8.
Two cubes each of volume 27 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid. (2011OD)
Solution:
Volume of a cube = 27 cm3
⇒ (Side)3 = (3)3 ∴ Side = 3 cm
Length of resulting cuboid, l = 2 × 3 = 6 cm
Breadth of resulting cuboid, b = 3 cm
Height of resulting cuboid, h = 3 cm
Surface area of resulting cuboid = 2(lb + bh + hl)
= 2(6 × 3 + 3 × 3 + 3 × 6)
= 2(18 + 9 + 18) = 2(45) = 90 cm2

Question 9.
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm, find the volume of the cylinder. (Use π = 227) (2016D)
Solution:
Let the radius and height of cylinder be r and h respectively
r + h = 37 cm …(i) [Given
Total surface area of cylinder = 1,628 cm2
2πr(r + h) = 1,628
⇒ 2πr(37) = 1,628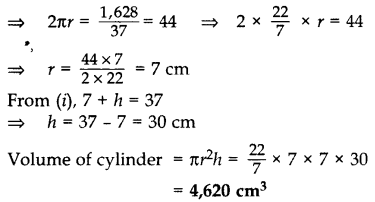

Question 10.
A right circular cone of radius 3 cm, has a curved surface area of 47.1 cm2. Find the volume of the cone. (Use π = 3.14) (2016D)
Solution:
C.S. Area of cone = 47.1 cm2 …[Given
…[Here, r = 3 cm
πrl = 47.1 = (3.14)(3)l = 47.1
Slant height, l =47.13.14(3) = 5 cm
⇒ r2 + h2 = l2 …[Pythagoras’ theorem
⇒ (3)2 + h2 = (5)2 ⇒ h2 = 25 – 9 = 16
⇒ h = +4 cm
Volume of the cone = 13πr2h = 13 (3.14)(3)2(4)
= 3.14(12) = 37.68 cm3

Question 11.
An icecream seller sells his icecreams in two ways: (2012OD)
(A) In a cone of r = 5 cm, h = 8 cm
(B) In a cup in shape of cylinder with r = 5 cm, h = 8 cm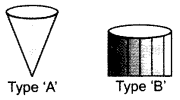

He charges the same price for both but prefers to sell his icecream in a cone.
(a) Find the volume of the cone and the cup.
(b) Which out of the two has more capacity?
Solution:
Volume of type ‘A’
Volume of cone + Volume of hemisphere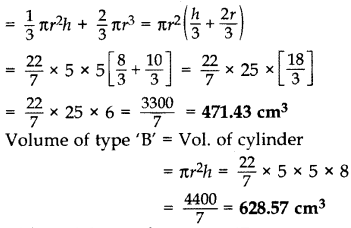

(a) ∴ Volume of a cone = 471.43 cm3
Volume of a cup = 628.57 cm3
(b) Cup has more capacity.

Question 12.
A vessel is in the form of a hemispherical bowl surmounted by a hollow cylinder of same diameter. The diameter of the hemispherical bowl is 14 cm and the total height of the vessel is 13 cm. Find the total (inner) suface area of the vessel. (Use π = 227) (2013D)
Solution: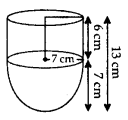

r = 142 = 7 cm
Inner surface area of the vessel = C.S. area of Hemi-sphere + C.S. area of Cylinder
= 2πr2 + 2πrh = 2πr(r + h) …C.S. area = curved surface area
= 2 × 227 × 77 + 6) = 44 × 13 = 572 cm2

Question 13.
A solid wooden toy is in the form of a hemisphere surmounted by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 16656 cm3. Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of ₹10 per cm2. [Use π = 227] (2015D)
Solution: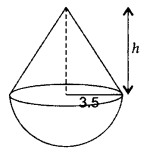

Let the height of cone = h
Radius of cone = Radius of hemisphere = r = 3.5 cm
Volume of solid wooden toy = Volume of hemisphere + Volume of cone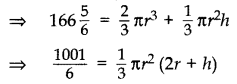

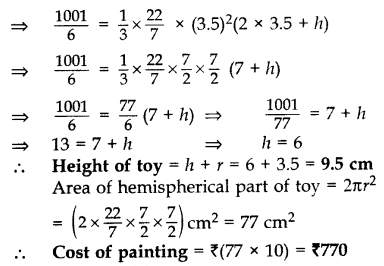
Question 14.
Due to sudden floods, some welfare associations jointly requested the government to get 100 tents fixed immediately and offered to contribute 50% of the cost. If the lower part of each tent is of the form of a cylinder of diameter 4.2 m and height 4 m with the conical upper part of same diameter but of height 2.8 m, and the canvas to be used costs 100 per sq. m, find the amount, the associations will have to pay. (Use π = 227) (2015OD)
Solution:
Let l be the slant height of cone
h be the height of cone = 2.8 m

Question 15.
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of ₹5 per 100 sq. cm. (Use π = 3.14) (2015OD)
Solution:
Let the side of cuboidal block (a) = 10 cm
Let the radius of hemisphere be r.
Side of cube = Diameter of hemisphere Largest possible diameter of hemisphere = 10 cm
∴ Radius, r = 102 = 5 cm
Total surface area = Total surface area of cube + Curved surface area of hemisphere- Area of base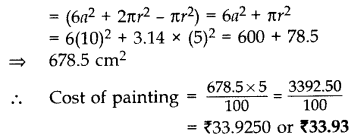

Question 16.
In Figure, is a decorative block, made up of two solids-a cube and a hemisphere. The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has a diameter of 3.5 cm. Find the total surface area of the block. (Use π = 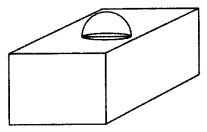227) (2016D)

Solution:
Total surface area of the block
= Total surface area of cube + C.S. Area of hemisphere – Area of circle
= 6(side)2 + 2πr2 – πr2
= 6(side)2 + πr2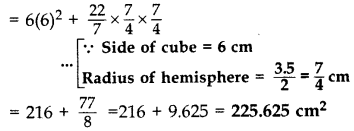

Question 17.
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel of base radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. (Use π = 227). (2016D)
Solution:
Let r and I be the radius and height of conical vessel i.e., 5 cm and 24 cm respectively.
Let H be the height of rise in water in cylindrical vessel and R be the radius, i.e., 10 cm.
Volume of water in cylindrical vessel = Volume of water in conical vessel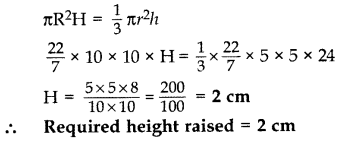

Question 18.
A milkman was serving his customers using two types of mugs A and B of inner diameter 5 cm to Mug‘A Mug‘B’ serve the customers. The height of the mugs is 10 cm. (2012D)
He decided to serve the customers in ‘B’ type of mug.
(a) Find the volume of the mugs of both types.
(b) Which mathematical concept is used in the above problem?

Solution:
(a) Let the radius of cylinder, hemi-sphere and cone be r сm
Let the height of cylinder and cone h1 and h2 respectively.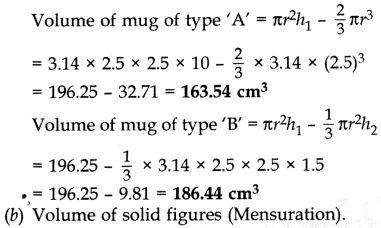

Question 19.
From a solid cylinder of height 7 cm and base diameter 12 cm, a conical cavity of same height and same base diameter is hollowed out. Find the total surface area of the remaining solid. [Use π = 227] (2012D)
Solution:

Question 20.
A wooden toy was made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the volume of wood in the toy. [Use π = 227] (2013D)
Solution:
Here r = 3.5 cm = 72 cm, h = 10 cm
Volume of wood in the toy = Volume of cylinder – 2(Vol. of hemisphere)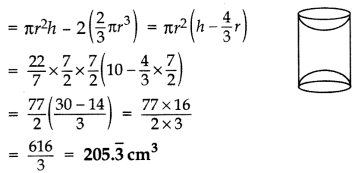

Question 21.
A solid cone of base radius 10 cm is cut into two parts through the mid-point of its height, by a plane parallel to its base. Find the ratio in the volumes of the two parts of the cone. (2013OD)
Solution:
Let BC = r сm and
DE = R = 10 cm
B and C are the mid-points of AD and AE respectively. …[Given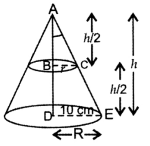

Question 22.
A solid metallic right circular cone 20 cm high and whose vertical angle is 60°, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 112 cm, find the length of the wire. (2014D)
Solution:
A solid cone AFE has been cut by BC || FE and
AD ⊥ FE.
∆ADF = ∆ADE (SSS)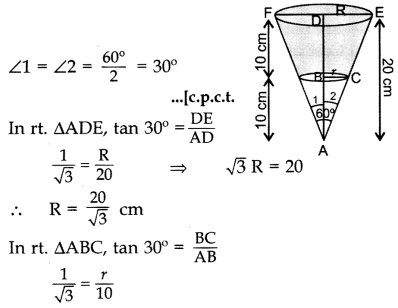

Question 23.
The largest possible sphere is carved out of a wooden solid cube of side 7 cm. Find the volume of the wood left. (Use π = 227) (2014OD)
Solution:
Volume of the wood left = Volume of cube – Volume of sphere

Question 24.
In Figure, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use π = 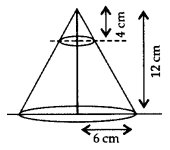227 and 3–√ = 2.236) (2015D)

Solution: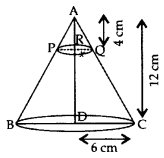

Let AR = 4 cm,
RD = 12 – 4 = 8 cm
Height of frustum (RD),
h = 8 cm Lower radius of frustum (DC),
r1 = 6 cm
We know, ∆ARQ ≅ ∆ADC

Question 25.
In Figure, from a cuboidal solid metallic block, of dimensions 15 cm × 10 cm × 5 cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block. (Use π =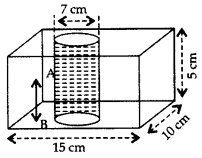227) (2015D)

Solution:
Let the length, breadth, height of cuboidal block be 15 cm, 10 cm and 5 cm respectively.
Total surface area of solid cuboidal block
= 2(lb + bh + lh)
= 2(15 × 10 + 10 × 5 + 15 × 5) cm2
= 2(150 + 50 + 75) = 2(275) = 550 cm2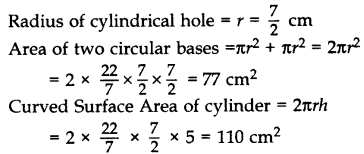

Required area = (Area of cuboidal block – Area of two circular bases + Area of cylinder)
= (550 + 110 – 77) cm2 = 583 cm2

Question 26.
A toy is in the shape of a solid cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 21 cm and 40 cm respectively, and the height of cone is 15 cm, then find the total surface area of the toy. [π = 3.14, be taken] (2011D)
Solution: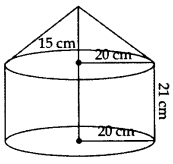

Height of cylinder, H = 21 cm
Height of cone, h = 15 cm
Common radius,

Question 27.
A cone of height 20 cm and radius of base 5 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the diameter of the sphere. (2011OD)
Solution:
Volume of the Sphere = Volume of Cone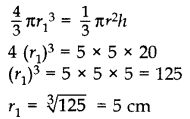

∴ Diameter of the sphere = 2r1 = 2(5) = 10 cm

Question 28.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, then find the radius and slant height of the heap. (2012D)
Solution:
Let x be radius of the conical heap.
Volume of conical heap = Volume of cyl. bucket

Question 29.
A solid metallic sphere of diameter 8 cm is melted and drawn into a cylindrical wire of uniform width. If the length of the wire is 12 m, find its width. (2013OD)
Solution:
Vol. of cylindrical wire = Volume of solid sphere

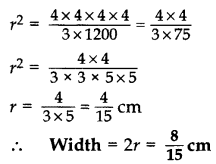
Question 30.
A well of diameter 4 m is dug 21 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 3 m to form an embankment. Find the height of the embankment. (2016D)
Solution:
Radius of well, r = 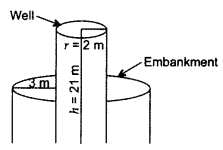42 = 2 m

Radius of embankment, R = 2 + 3 = 5 m
Height of the well, h = 21 m
Required height raised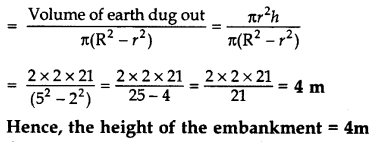

Question 31.
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 359 cm. Find the diameter of the cylindrical vessel. (2016D)
Solution:
Radius of sphere, r = 122 = 6 cm
Let h be the height of risen water level i.e., 3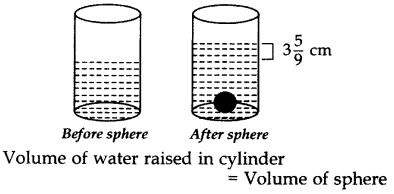59cm or 329 cm and R be the radius of cylindrical vessel.

Question 32.
A solid sphere of radius 10.5 cm is melted and recast into smaller solid cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed. (Use π = 227) (2012 OD)
Solution: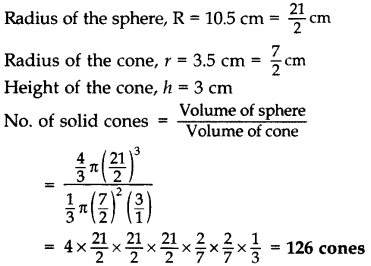

Question 33.
The 34th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in cylindrical vessel. (2017D)
Solution: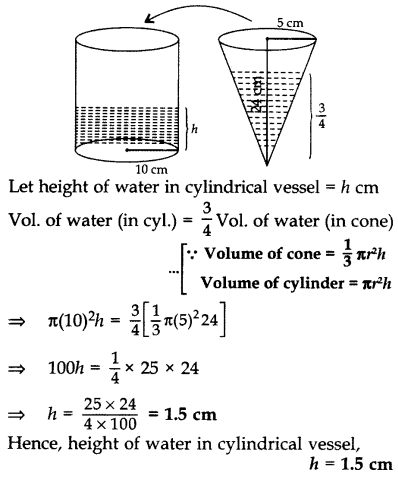

Question 34.
504 cones, each of diameter 3.5 cm and height 3cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area. (Use π = 227) (2015OD)
Solution:
Let the radius of sphere (R) = ?
Let the radius of cone (r) = 3.52 = 3520
Let the height of cone (h) = 3 cm
Volume of metal in 1 cone = 13πr2h
Volume of metal in 504 cones

Question 35.
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank which is 10 m in diameter and 2 m deep. If the water flows through the pipe at the rate of 4 km per hour, in how much time will the tank be filled completely? (2014D)
Solution:

Question 36.
Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/h. How much area will it irrigate in 10 minutes, if 8 cm of standing water is needed for irrigation? (2014OD)
Solution:
Speed of water = 4 km/hr
Canal, l = 4 × 1060 = 23km

Question 37.
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of the each bottle, if 10% liquid is wasted in this transfer. (2015OD)
Solution:
Let the radius of hemispherical bowl,
(R) = 362 = 18 cm
Let the radius of cylindrical bottle (r) = 62 = 3 cm
Let the height of cylindrical bottle be h = ?
Vol. of liquid in the hemispherical bowl = 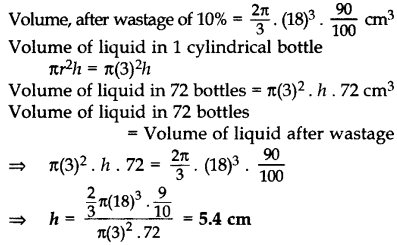23πR3

Question 38.
An open metal bucket is in the shape of a frustum of a cone of height 21 cm with radii of its lower and upper ends as 10 cm and 20 cm respectively. Find the cost of milk which can completely fill the bucket at ₹30 per litre. [Use π = 227] (2011OD)
Solution:
Here h = 21 cm, r = 10 cm, R = 20 cm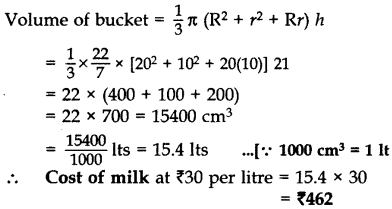

Question 39.
A toy is in the form of a cone mounted on a hemisphere of same radius 7 cm. If the total height of the toy is 31 cm, find its total surface area. (Use π = 227) (2013OD)
Solution: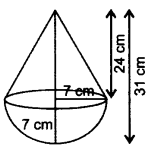

Radius = 7 cm
Vertical height of cone,
h = 31 – 7 = 24 cm
Slant height,

Question 40.
In Figure, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of ₹500/sq. metre. (Use π = 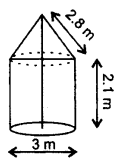227) (2016OD)

Solution:

Surface Areas and Volumes Class 10 Important Questions Long Answer (4 Marks)

Question 41.
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid. [Use π = 227) (2012D)
Solution:
Radius, r = 7 cm
Height of cone, h = 2(7) = 14 cm
Volume of solid = Vol. of hemisphere + Volume of cone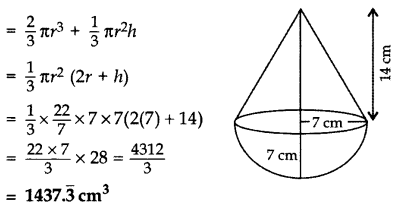

Question 42.
A hemispherical tank, full of water, is emptied by a pipe at the rate of 257 litres per sec. How much time will it take to empty half the tank if the diameter of the base of the tank is 3 m? (2012OD)
Solution:

Question 43.
Water is flowing through a cylindrical pipe, of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m/s. Determine the rise in level of water in the tank in half an hour. (2013D)
Solution:
Radius of tank, r1 = 40 cm
Internal radius of cylindrical pipe, r2 = 22 = 1 cm
Let the height of rises water, h1 = ?
Length of water flow in 1 second = 0.4 m
= 410 × 100 = 40 cm
∴ Length of water flow in 30 minutes, h2
= 40 × 60 × 30 = 72,000 cm
Volume of water in cylinder tank
= Volume of water flow from cylindrical pipe in half an hour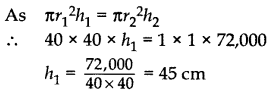

∴ Level of water in cylinder tank rises in half an hour, h1 = 45 cm

Question 44.
150 spherical marbles, each of diameter 1.4 cm, are dropped in a cylindrical vessel of diameter 7 cm containing some water, which are completely immersed in water. Find the rise in the level of water in the vessel. (2014OD)
Solution:

Question 45.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid. (Take π = 227) (2014D)
Solution:

Question 46.
Water is flowing at the rate of 2.52 km/hr. through a cylindrical pipe into a cylindrical tank, the radius of whose base is 40 cm. If the increase in the level of water in the tank, in half an hour is 3.15 m, find the internal diameter of the pipe. (2015D)
Solution:
Let r be the internal radius of the pipe.
Radius of base of tank, R = 40 cm
= 40100=25 m
Level of water raised in the tank (H) = 3.15 m
If the flow rate in an hour = 2.52 km = 2520 m
Then, the flow rate in half an hour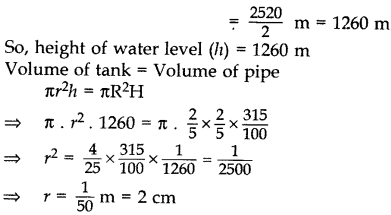

∴ Internal diameter of pipe = 2r = 2 × 2 = 4 cm
∴ Internal diameter of pipe = 4 cm

Question 47.
From each end of a solid metal cylinder, metal was scooped out in hemispherical form of same diameter. The height of the cylinder is 10 cm and its base is of radius 4.2 cm. The rest of the cylinder is melted and converted into a cylindrical wire of 1.4 cm thickness. Find the length of the wire. [Use π = 227] (2015OD)
Solution:
Let h be the height of cylinder = 10 cm
Let r be the radius of cylinder = 4.2 cm
Radius of cylinder
= Radius of hemispherical metal = r = 4.2 cm ..[Given
Total Volume of cylinder = πr2h

Question 48.
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (Use π = 3.14) (2016D)
Solution:
Radius of the top of bucket, R = 20 cm
Radius of the bottom of bucket, r = 12 cm
Voulume of bucket = 12308.8 cm3

Question 49.
A container shaped like a right circular cylinder having base radius 6 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm and radius 3 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream. (2012D)
Solution:
Volume of cylinder = πr2h
Volume of ice-cream cone = 1/3 πr21h1
Volume of hemispherical top of ice-cream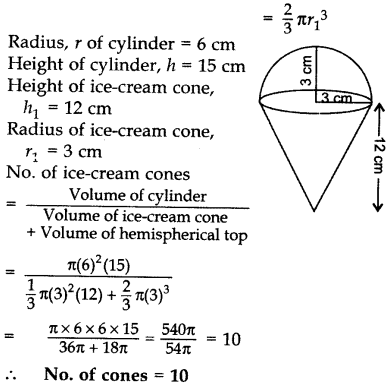

Question 50.
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m. (2012OD)
Solution:

Question 51.
A well of diameter 4 m is dug 14 m deep. The earth taken out is spread evenly all around the well to form a 40 cm high embankment. Find the width of the embankment. (2015D)
Solution:
Let h be the height of well and r be the radius of well.
h = 14 m, r= d2=42 = 2 m
Volume of earth taken out after digging the well = πr2h
= (227×2×2×14) m3 = 176 m3 …(i)
Let x be the width of embankment formed by using (i),
∴ Total width of well including embankment (R) = 2 + x
Height of embankment (H) = 40 cm = 40100 m
Volume of well = Volume of embankment So, Volume of embankment = T(R2 – r2)H = 176 …[From (i)

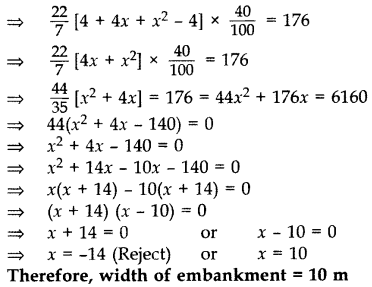
Question 52.
A tent consists of a frustum of a cone, surmounted by a cone. If the diameter of the upper and lower circular ends of the frustum be 14 m and 26 m respectively, the height of the frustum be 8 m and the slant height of the surmounted conical portion be 12 m, find the area of canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of surmounted conical portion are equal). (2014OD)
Solution:
Upper radius of frustum of a cone,

Question 53.
Water is flowing at the rate of 15 km/hour through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in the pond rise by 21 cm? (2011OD)
Solution:
H = 15 km = 15000 m (1 km = 1000 m)
Radius of pipe (t) = 142 = 7 cm = 7100 m
Volume of pipe (cylinder) = πr2H
∴ Volume of water flowing through the cylindrical pipe in an hour at the rate of 15 km/hr.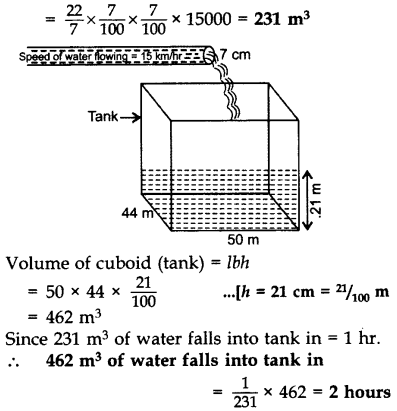

Question 54.
Water is flowing at the rate of 10 km/hour through a pipe of diameter 16 cm into a cuboidal tank of dimensions 22 m × 20 m × 16 m. How long will it take to fill the empty tank? [Use π = 227] (2011OD)
Solution:

Question 55.
A drinking glass is in the shape of the frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [Use π = 227] (2012OD)
Solution: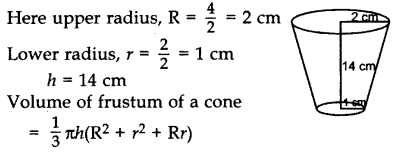

Question 56.
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of 10 per 100 cm2. (Use π = 3.14) (2013D)
Solution:
Depth of bucket, h = 24 cm
Radius of top bucket,

Question 57.
The slant height of a frustum of a cone is 4 cm and the perimeters of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum. (2017OD)
Solution:
Let longer radius = R cm
Smaller radius = r cm
2πR = 18 and 2πr = 6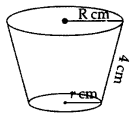

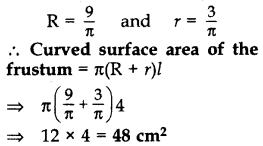
Question 58.
Sushant has a vessel, of the form of an inverted cone, open at the top, of height 11 cm and radius of top as 2.5 cm and is full of water. Metallic spherical balls each of diameter 0.5 cm are put in the vessel due to which 25 th  of the water in the vessel flows out. Find how many balls were put in the vessel. Sushant made the arrangement so that the water that flows out irrigates the flower beds. (2014D)
Solution:
Numbers of spherical balls

Question 59.
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m × 11 m. Find the height of the platform. (Use π = 227] (2015D)
Solution:
Let h be the height of well, h = 21 m

Question 60.
The dimensions of a solid iron cuboid are 4.4 m × 2.6 m × 1.0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe. (2017OD)
Solution: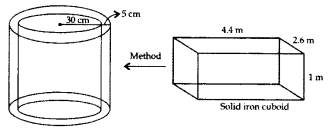

Inner radius, r = 30 cm = 0.30 m
Outer radius, R = (30 + 5) cm = 35 cm or 0.35 m
As per the question: (Volume of hollow Cylindrical pipe) = (Volume of solid iron cuboid)

Question 61.
In a rain-water harvesting system, the rain water from a roof of 22 m × 20 m drains into a cylindrical tank having diameter of base 2 m and height 3.5 m. If the tank is full, find the rainfull in cm. (2017OD)
Solution:
Let the rainfall be x m.
Volume of water on the roof = Volume of cylindrical tank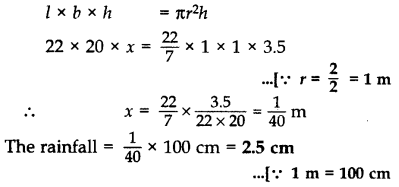

Question 62.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. (Use π = 227) (2012D)
Solution:
Here R = 28 cm, r = 21 cm
Volume of Bucket = 28.49 litres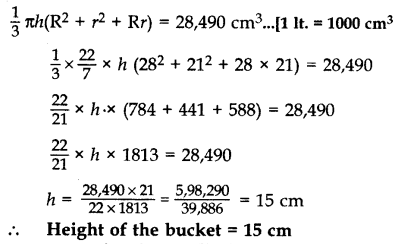

Question 63.
Water running in a cylindrical pipe of inner diameter 7 cm, is collected in a container at the rate of 192.5 litres per minute. Find the rate of flow of water in the pipe in km/h. (Use π = 227) (2013OD)
Solution:
Volume of water that flows for one hour
= (192.50 × 60) Its.
= 192.50 × 60 × 1000 cm3 …[∵ 1 lt. 1000 cm3
Inner radius of the cylindrical pipe = 72 cm
Let h cm be the length of the volume of water that flows in one hour.
Volume of water that flows in 1 hr. = πr2h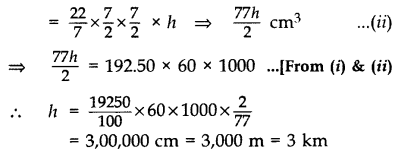

Hence the rate of flow of water in the pipe = 3 km/hr.

Question 64.
Due to heavy floods in a State, thousands were rendered homeless. 50 schools collectively offered to the State Government to provide place and the canvas for 1,500 tents to be fixed by the Government and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 m and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents coşts ₹120 per sq. m, find the amount shared by ‘each school to set up the tents. (2016OD)
Solution: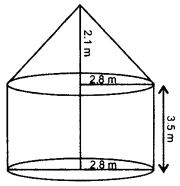

Let r and h be the radius and height of cylindrical part respectively and I be the slant height of conical part.
Slant height of conical part (l),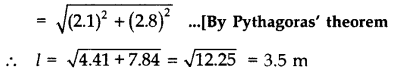

Question 65.
A container, open at the top and made up of metal sheet is in the form of a frustum of a cone of height 16 cm with diameters of its lower and upper ends as 16 cm and 40 cm respectively. Find the cost of metal sheet used to make the container, if it costs 10 per 100 cm2. [Take a = 3.14] (2013OD)
Solution:
Height of frustum of a cone, h = 16 cm

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

Important Questions & Answers For Class 10 Maths Chapter 13 Surface Areas and Volumes

Q.1: Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere. The entire top is 5 cm in height, and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π = 22/7)

Solution:

TSA of the toy = CSA of hemisphere + CSA of cone

Curved surface area of the hemisphere = 1/ 2 (4πr2) = 2π r2 = 2(22/7)× (3.5/2) × (3.5/2) = 19.25 cm2

Height of the cone = Height of the top – Radius of the hemispherical part

= (5 – 3.5/2) cm = 3.25 cm

Sant height of the cone (l) =r2+h2−−−−−−√=(3.52)2+(3.25)2−−−−−−−−−−−−√=3.7 cm (approx.)

Therefore, CSA of cone = πrl = (22/7) × (3.5/2) × 3.7 = 20.35 cm2

Hence, the surface area of the top = [2(22/7)× (3.5/2) × (3.5/2) + (22/7) × (3.5/2) × 3.7] cm2

= (22/7) × (3.5/2) (3.5+3.7) cm2

= (11/2) × (3.5 + 3.7) cm2

= 39.6 cm2 (approx.)

Q. 2: Mayank made a bird-bath for his garden in the shape of a cylinder with a hemispherical depression at one end, as shown in the figure. The height of the cylinder is 1.45 m, and its radius is 30 cm. Find the total surface area of the bird-bath. (Take π = 22/7)

Solution:

Let h be the height of the cylinder and r be the common radius of the cylinder and hemisphere. Then, the total surface area of the bird-bath = CSA of cylinder + CSA of the hemisphere

= 2πrh + 2πr2

= 2π r(h + r)

= 2 (22/7) × 30 × (145 + 30) cm2

= 33000 cm2 = 3.3 m2

Q. 3: 2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.

Solution:

The diagram will obtain as below:

Given,

The Volume (V) of each cube is = 64 cm3

This implies that a3 = 64 cm3

∴ The side of the cube, i.e. a = 4 cm

Also, the breadth and length of the resulting cuboid will be 4 cm each while its height will be 8 cm.

So, the surface area of the cuboid (TSA) = 2(lb + bh + lh)

Now, by putting the values, we get,

= 2(8×4 + 4×4 + 4×8) cm2

= (2 × 80) cm2

Hence, TSA of the cuboid = 160 cm2

Q. 4: A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m2. (Note that the base of the tent will not be covered with canvas.)

Solution:

It is known that a tent is a combination of a cone and a cylinder, as shown below.

From the question, we know that

The diameter = D = 4 m

l = 2.8 m (slant height)

The radius of the cylinder is equal to the radius of the cylinder

So, r = 4/2 = 2 m

Also, we know the height of the cylinder (h) is 2.1 m

So, the required surface area of the given tent = surface area of the cone (the top) + surface area of the cylinder(the base)

= πrl + 2πrh

= πr (l+2h)

Now, substituting the values and solving it we get the value as 44 m2

∴ The cost of the canvas at the rate of Rs. 500 per m2 for the tent will be

= Surface area × cost/ m2

= 44 × 500

So, Rs. 22000 will be the total cost of the canvas.

Q. 5: A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm, and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference between the volumes of the cylinder and the toy. (Take π = 3.14)

Solution:

Let BPC be the hemisphere and ABC be the cone standing on the base of the hemisphere as shown in the above figure.

The radius BO of the hemisphere (as well as of the cone) =( ½) × 4 cm = 2 cm.

So, volume of the toy = (⅔) πr3 + (⅓) πr2h

= (⅔) × 3.14 × 23 + (⅓)× 3.14 × 22 × 2

= 25.12 cm3

Now, let the right circular cylinder EFGH circumscribe the given solid.

The radius of the base of the right circular cylinder = HP = BO = 2 cm, and its height is

EH = AO + OP = (2 + 2) cm = 4 cm

So, the volume required = volume of the right circular cylinder – the volume of the toy

= (3.14 × 22 × 4 – 25.12) cm3

= 25.12 cm3

Hence, the required difference between the two volumes = 25.12 cm3

Q. 6: A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.

Solution:

Given,

For the cylinder part, Height (h) = 8 cm and Radius (R) = (2/2) cm = 1 cm

For the spherical part, Radius (r) = (8.5/2) = 4.25 cm

Now, the volume of this vessel = Volume of cylinder + Volume of a sphere

= π × (1)2 × 8 + (4/3) π (4.25)3
= 25.12 + 321.6
= 346.67 cm3

Q. 7: A cone of height 24 cm and radius of base 6 cm is made up of modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.

Solution:

The volume of cone = (⅓) × π × 6 × 6 × 24 cm3

If r is the radius of the sphere, then its volume is (4/3) πr3.

Since the volume of clay in the form of the cone and the sphere remains the same, we

Have (4/3) πr3 = (⅓) × π × 6 × 6 × 24 cm3

r3 = 3 × 3 × 24 = 33 × 23

So, r = 3 × 2 = 6

Therefore, the radius of the sphere is 6 cm.

Q. 8: Selvi’s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 95cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water from the sump which had been full. Compare the capacity of the tank with that of the sump. (Use π = 3.14)

Solution:

The volume of water in the overhead tank equals the volume of the water removed from the sump.

Now, the volume of water in the overhead tank (cylinder) = πr2h

= 3.14 × 0.6 × 0.6 × 0.95 m3

The volume of water in the sump when full = l × b × h = 1.57 × 1.44 × 0.95 m3

The volume of water left in the sump after filling the tank

= [(1.57 × 1.44 × 0.95) – (3.14 × 0.6 × 0.6 × 0.95)] m3 = (1.57 × 0.6 × 0.6 × 0.95 × 2) m3

Height of the water left in the sump = (volume of water left in the sump)/ (l × b)

= (1.57× 0.6× 0.6× 0.95 ×2)/ (1.57 ×1.44)

= 0.475 m

= 47.5 cm

Capacity of tank / Capacity of sump = (3.14 × 0.6 × 0.6 × 0.95)/ (1.57 × 1.44 × 0.95)

=1/ 2

Therefore, the capacity of the tank is half the capacity of the sump.

Q. 9: Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.

Solution:

For Sphere 1:

Radius (r1) = 6 cm

∴ Volume (V1) = (4/3) × π× r13

For Sphere 2:

Radius (r2) = 8 cm

∴ Volume (V2) = (4/3) × π × r23

For Sphere 3:

Radius (r3) = 10 cm

∴ Volume (V3) = (4/3) × π× r33

Also, let the radius of the resulting sphere be “r”

Now, Volume of resulting sphere = V1 + V2 + V3

(4/3)× π× r3 = (4/3)× π× r13 + (4/3)× π× r23 + (4/3) × π× r33

r3 = 63 + 83 + 103

r3 = 1728

r = 12 cm

Q. 10: An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet as shown in the figure. The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold. (Take π = 22/7)

Solution:

The total height of the bucket = 40 cm, which includes the height of the base.

So, the height of the frustum of the cone = (40 – 6) cm = 34 cm.

Therefore, the slant height of the frustum, l=h2+(r1−r2)2−−−−−−−−−−−−√

where r1 = 22.5 cm, r2 = 12.5 cm and h = 34 cm.

l=342+(22.5–12.5)2−−−−−−−−−−−−−−−√ =342+102−−−−−−−−√

=35.44 cm

The area of metallic sheet used = curved surface area of frustum of cone + area of circular base + curved surface area of cylinder

= [π × 35.44 (22.5 + 12.5) + π × (12.5)2 + 2π × 12.5 × 6] cm2

= 22/7 (1240.4 + 156.25 + 150) cm2

= 4860.9 cm2

Now, the volume of water that the bucket can hold (also, known as the capacity

of the bucket)

= (πh)/3 × (r12 + r22 + r1r2)

=(22/7) × (34/3) × [(22.5)2 + (12.5)2 + (22.5)(12.5)]

=(22/7) × (34/3) × 943.75

= 33615.48 cm3

= 33.62 litres (approx.)

Q. 11: A cylindrical pencil sharpened at one edge is the combination of

(A) a cone and a cylinder

(B) frustum of a cone and a cylinder

(C) a hemisphere and a cylinder

(D) two cylinders.

Solution:

(A) a cone and a cylinder

The Nib of a sharpened pencil = conical shape

The rest of the part of a sharpened pencil = cylindrical

Therefore, a pencil is a combination of a cylinder and a cone.

Q. 12: A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing at a speed of 20 km/h. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired?

Solution:

The volume of water flows in the canal in one hour = width of the canal × depth

of the canal × speed of the canal water = 3 × 1.2 × 20 × 1000 m3

= 72000m3

In 20 minutes the volume of water = (72000 × 20)/ 60 = 24000 m3

Area irrigated in 20 minutes, if 8 cm, i.e., 0.08 m standing water is required

=24000/0.08

= 300000 m2

= 30 hectares