NEW LEARNET EDUCATION
Chapter - 6
Triangle ( Handwritten MCQ )
MCQ PART - 1
1. Which of the following triangles have the same side lengths?
(a)Scalene
(b)Isosceles
(c)Equilateral
(d)None of these
Answer: (c)
Explanation: Equilateral triangles have all its sides and all angles equal.
2. Area of an equilateral triangle with side length a is equal to:
(a)√3/2a
(b)√3/2a2
(c)√3/4 a2
(d)√3/4 a
Answer: c √3/4 a2
3.D and E are the midpoints of side AB and AC of a triangle ABC, respectively and BC=6cm. If DE || BC, then the length of DE is:
(a)2.5
(b)3
(c)5
(d)6
Answer: b
Explanation: By midpoint theorem,
DE=½ BC
DE = ½ of 6
DE=3cm
4. The diagonals of a rhombus are 16cm and 12cm, in length. The side of rhombus in length is:
(a)20cm
(b)8cm
(c)10cm
(d)9cm
Answer: c
Explanation: Here, half of the diagonals of a rhombus are the sides of the triangle and side of the rhombus is the hypotenuse.
By Pythagoras theorem,
(16/2)2+(12/2)2=side2
82+62=side2
64+36=side2
side=10cm
5. Corresponding sides of two similar triangles are in the ratio of 2:3. If the area of small triangle is 48 sq.cm, then the area of large triangle is:
(a)230 sq.cm.
(b)106 sq.cm
(c)107 sq.cm.
(d)108 sq.cm
Answer: d
Solution: Let A1 and A2 are areas of the small and large triangle.
Then,
A2/A1=(side of large triangle/side of small triangle)
A2/48=(3/2)2
A2=108 sq.cm.
6. If perimeter of a triangle is 100cm and the length of two sides are 30cm and 40cm, the length of third side will be:
(a)30cm
(b)40cm
(c)50cm
(d)60cm
Answer: a
Solution: Perimeter of triangle = sum of all its sides
P = 30+40+x
100=70+x
x=30cm
7. If triangles ABC and DEF are similar and AB=4cm, DE=6cm, EF=9cm and FD=12cm, the perimeter of triangle is:
(a)22cm
(b)20cm
(c)21cm
(d)18cm
Answer: d
Explanation: ABC ~ DEF
AB=4cm, DE=6cm, EF=9cm and FD=12cm
AB/DE = BC/EF = AC/DF
4/6 = BC/9 = AC/12
BC = (4.9)/6 = 6cm
AC = (12.4)/6 = 8cm
Perimeter = AB+BC+AC
= 4+6+8
=18cm
8. The height of an equilateral triangle of side 5cm is:
(a)4.33
(b)3.9
(c)5
(d)4
Answer: a
Explanation:The height of the equilateral triangle ABC divides the base into two equal parts at point D.
Therefore,
BD=DC= 2.5cm
In triangle ABD, using Pythagoras theorem,
AB2=AD2+BD2
52=AD2+2.52
AD2 = 25-6.25
AD2=18.75
AD=4.33 cm
9. If ABC and DEF are two triangles and AB/DE=BC/FD, then the two triangles are similar if
(a)∠A=∠F
(b)∠B=∠D
(c)∠A=∠D
(d)∠B=∠E
Answer: b
10. Sides of two similar triangles are in the ratio 4: 9. Areas of these triangles are in the ratio
(a)2: 3
(b)4: 9
(c)81: 16
(d)16: 81
Answer: d
Explanation: Let ABC and DEF are two similar triangles, such that,
ΔABC ~ ΔDEF
And AB/DE = AC/DF = BC/EF = 4/9
As the ratio of the areas of these triangles will be equal to the square of the ratio of the corresponding sides,
∴ Area(ΔABC)/Area(ΔDEF) = AB2/DE2
∴ Area(ΔABC)/Area(ΔDEF) = (4/9)2 = 16/81 = 16: 81
MCQ PART - 2
1. O is a point on side PQ of a APQR such that PO = QO = RO, then
(a) RS² = PR × QR
(b) PR² + QR² = PQ²
(c) QR² = QO² + RO²
(d) PO² + RO² = PR²
Answer
Answer: b
2. In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to
(a) 7.5 cm
(b) 3 cm
(c) 4.5 cm
(d) 6 cm
Answer
Answer: c
3. AABC is an equilateral A of side a. Its area will be…
Answer
Answer: a
4. In a square of side 10 cm, its diagonal = …
(a) 15 cm
(b) 10√2 cm
(c) 20 cm
(d) 12 cm
Answer
Answer: b
5. In a rectangle Length = 8 cm, Breadth = 6 cm. Then its diagonal = …
(a) 9 cm
(b) 14 cm
(c) 10 cm
(d) 12 cm
Answer
Answer: c
6. In a rhombus if d1 = 16 cm, d2 = 12 cm, its area will be…
(a) 16 × 12 cm²
(b) 96 cm²
(c) 8 × 6 cm²
(d) 144 cm²
Answer
Answer: b
7. In a rhombus if d1 = 16 cm, d2 = 12 cm, then the length of the side of the rhombus is
(a) 8 cm
(b) 9 cm
(c) 10 cm
(d) 12 cm
Answer
Answer: c
8. If in two As ABC and DEF,
(a) ∆ABC ~ ∆DEF
(b) ∆ABC ~ ∆EDF
(c) ∆ABC ~ ∆EFD
(d) ∆ABC ~ ∆DFE
Answer
Answer: d
9. It is given that ∆ABC ~ ∆DEF and
(а) 5
(b) 25
(c)
(d)
Answer
Answer: b
10. In ∠BAC = 90° and AD ⊥ BC. A Then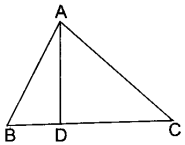
(а) BD.CD = BC²
(б) AB.AC = BC²
(c) BD.CD = AD²
(d) AB.AC = AD²
Answer
Answer: c
11. D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is
(a) 2.5
(b) 3
(c) 5
(d) 6
Answer
Answer: b
12. If ΔABC ~ ΔDEF and ΔABC is not similar to ΔDEF then which of the following is not true?
(a) BC.EF = AC.FD
(b) AB.ED = AC.DE
(c) BC.DE = AB.EE
(d) BC.DE = AB.FD
Answer
Answer: c
13. If in two triangles DEF and PQR, ZD = ZQ and ZR = ZE, then which of the following is not true?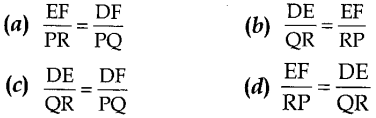
Answer
Answer: b
14. If ΔABC ~ ΔPQR,
(a) 9
(b) 3
(c) 1/3
(d) 1/9
Answer
Answer: a
15. If ΔABC ~ ΔQRP, AB = 18 cm and BC = 15 cm, then PR is equal to
(a) 10 cm
(b) 12 cm
(c)
(d) 8 cm
Answer
Answer: a
16. If in triangles ABC and DEF,
(a) ∠B = ∠E
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠A = ∠F
Answer
Answer: c
17. In the given figure, 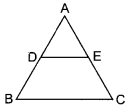
(a) 70°
(b) 50°
(c) 80°
(d) 60°
Answer/Explanation
Answer: d
Explaination:
∵ DE || BC
∴ ∠ABC = 70°.
(Corresponding angles) Using angle sum property of triangle ∠ABC + ∠BCA + ∠BAC = 180° ∠BCA = 60°.
18. In given figure, AD = 3 cm, AE = 5 cm, BD = 4 cm, CE = 4 cm, CF = 2 cm, BF = 2.5 cm, then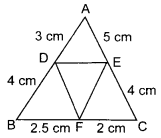
(a) DE || BC
(b) DF || AC
(c) EF || AB
(d) none of these
Answer/Explanation
Answer: c
Explaination:
19. If ΔABC ~ ΔEDF and ΔABC is not similar to ΔDEF, then which of the following is not true? [NCERT Exemplar Problems]
(a) BC . EF = AC . FD
(b) AB . EF = AC . DE
(c) BC . DE = AB . EF
(d) BC . DE = AB . FD
Answer/Explanation
Answer: c
Explaination:
20. If in two triangles ABC and PQR,
(a) ΔPQR ~ ΔCAB
(b) ΔPQR ~ ΔABC
(c) ΔCBA ~ ΔPQR
(d) ΔBCA ~ ΔPQR
Answer/Explanation
Answer: a
Explaination: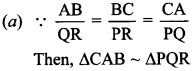
21. Match the column:
(a) 1 → A, 2 → B, 3 → C, 4→ D
(b) 1 → D, 2 → A, 3 → C, 4 → B
(c) 1 → B, 2 → A, 3 → C, 4 → D
(d) 1 → C, 2 → B, 3 → D, 4 → A.
Answer/Explanation
Answer: c
Explaination:
(c) Properties of triangles
22. In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are [NCERT Exemplar Problems]
(a) congruent but not similar
(b) similar but not congruent
(c) neither congruent nor similar
(d) congruent as well as similar
Answer/Explanation
Answer: b
Explaination: (b) Similar but not congruent
23. If in triangles ABC and DEF,
(a) ∠B = ∠E
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠A = ∠F
Answer/Explanation
Answer: c
Explaination: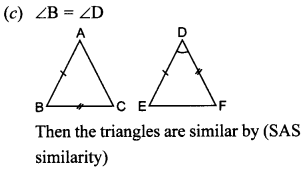
24. ABC and BDE are two equilateral triangles such that D is mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(a) 2 : 1
(b) 1:4
(c) 1:2
(d) 4:1
Answer/Explanation
Answer: d
Explaination: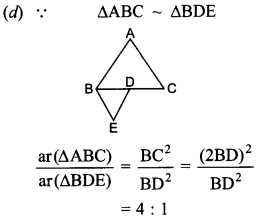
25. Sides of two similar triangles are in the ratio 3 : 7. Areas of these triangles are in the ratio
(a) 9 : 35
(b) 9 : 49
(c) 49 : 9
(d) 9 : 42
Answer/Explanation
Answer: b
Explaination:
(b) Ratio of areas of two similar triangles is the square of the ratio of their corresponding sides.
Required ratio = 9 : 49.
26. Sides of triangles are (i) 3 cm, 4 cm, 6 cm. (ii) 4 cm, 5 cm, 6 cm. (iii) 7 cm, 24 cm, 25 cm (iv) 5 cm, 12 cm, 14 cm. Which of these is right triangle?
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Answer/Explanation
Answer: c
Explaination:
On verification, triangle with sides 7 cm, 24 cm and 25 cm is a right triangle
∵ (25)² = (7)² + (24)².
27. If in two triangles DEF and PQR, ZD = ZQ and ZR = ZE, then which of the following is not true?
Answer/Explanation
Answer: b
Explaination: (b) Because ΔDEF ~ ΔQRP
28. “If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.” This theorem is known as _____ .
Answer/Explanation
Answer:
Explaination:
Thales Theorem or Basic Proportionality Theorem
29. In ΔABC, D and E are points on sides AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 6.6 cm then find AC.
Answer/Explanation
Answer:
Explaination: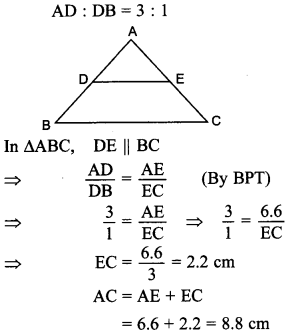
30. In the given figure, value of x (in cm) is _____ .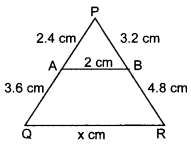
Answer/Explanation
Answer:
Explaination:
31. In the given figure, if ΔABC ~ ΔPQR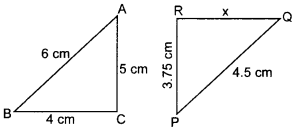
The value of x is_____ .
Answer/Explanation
Answer:
Explaination: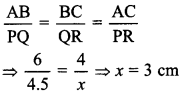
32. The perimeter of two similar triangles ABC and LMN are 60 cm and 48 cm respectively. If LM = 8 cm, then what is the length of AB?
Answer/Explanation
Answer:
Explaination:
33. In fig. ZM = ZN = 46°, express x in terms of a, b and c, where a, b and c are lengths of LM, MN and NK respectively.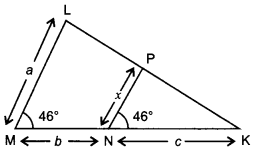
Answer/Explanation
Answer:
Explaination:
34. ΔABC ~ ΔPQR. Area of ΔABC = 81 cm² and area of ΔPQR =121 cm². If altitude AD = 9 cm, then PM = ______ .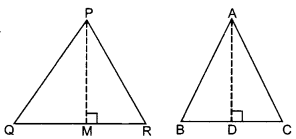
Answer/Explanation
Answer:
Explaination: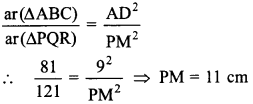
35. Given ΔABC ~ ΔPQR, if
Answer/Explanation
Answer:
Explaination:
36. In fig., DE || BC, AD = 1 cm and BD = 2 cm. What is the ratio of the ar(ΔABC) to the ar(ΔADE)? [Delhi 2019]
Answer/Explanation
Answer:
Explaination:
Given: In ΔABC, DE || BC
Also AD = 1 cm and BD = 2 cm
To find: ar(ΔABC) : ar(ΔADE)
As DE || BC (Given)
∠D = ∠B and ∠E = ∠C (Corresponding angles)
∴ ΔADE ~ ΔABC (By AA similarity)
ar(ΔABC) : ar(ΔADE) = 9:1.
37. In figure, S and T are points on the sides PQ and PR, respectively of APQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.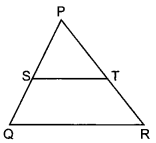
Answer/Explanation
Answer:
Explaination:
S and T are points on the sides PQ and PR of ΔPQR and PT = 2 cm, TR = 4 cm, ST || QR
In APST and ΔPQR,
∠S = ∠Q (Corresponding angles)
∠P = ∠P (Common)
∴ ΔPST ~ ΔPQR (AA similarity)
38. In ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm. The angle B is _____ .
Answer/Explanation
Answer:
Explaination: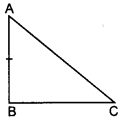
AC² = 144 cm²
AB² = 108 cm²
BC² = 36 cm²
Now, AB² + BC²
= 144 = AC² B
∴ ∠B = 90°
39. The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is
(a) 9 cm
(b) 10 cm
(c) 8 cm
(d) 20 cm
Answer/Explanation
Answer: b
Explaination:
Diagonals of a Rhombus are perpendicular to each other and bisect each oSo AO = 8 cm
BO = 6 cm
∠AOB = 90°
In right angled ΔAOB
AB² = AO² + OB²
AB² = 8² + 6² = 64 + 36
AB =√100 = 10 cm.
40. The sides of a triangle are 30, 70 and 80 units. If an altitude is droped upon the side of length 80 units, the larger segment cut off on this side is______.
Answer/Explanation
Answer:
Explaination: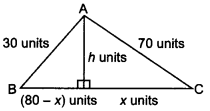
Now h² = 30² – (80 – x)²
Also h² = 70² – x²
⇒ 30² – (80 – x)² = 70² – x²
⇒ 160x = 10400
⇒ x=65 units.
41. In Fig., ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.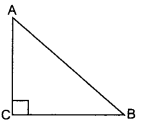
Answer/Explanation
Answer:
Explaination:
Given: AC = 4 cm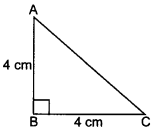
For isosceles triangle,
AC = BC
∴ BC = 4 cm
Using Pythagoras theorem,
AB² = AC2 + BC²
AB² = (4)2 + (4)²
⇒ AB² = 16 + 16 = 32
⇒ AB = A√32 = 4√2 cm.



0 Comments